10003. Cutting Sticks

You have to cut a wood stick into pieces. The most affordable company, The Analog Cutting Machinery, Inc. (ACM), charges money according to the length of the stick being cut. Their procedure of work requires that they only make one cut at a time.

It is easy to notice that different selections in the order of cutting can led to different prices. For example, consider a stick of length 10 meters that has to be cut at 2, 4 and 7 meters from one end. There are several choices. One can be cutting first at 2, then at 4, then at 7. This leads to a price of 10 + 8 + 6 = 24 because the first stick was of 10 meters, the resulting of 8 and the last one of 6. Another choice could be cutting at 4, then at 2, then at 7. This would lead to a price of 10 + 4 + 6 = 20, which is a better price.

Your boss trusts your computer abilities to find out the minimum cost for cutting a given stick.

Input. The input will consist of several input cases. The first line of each test case will contain a positive number l that represents the length of the stick to be cut. You can assume l < 1000. The next line will contain the number n (n < 50) of cuts to be made.

The next line consists of n positive numbers c_i (0 < c_i < l) representing the places where the cuts have to be done, given in strictly increasing order.

An input case with l = 0 will represent the end of the input.

Output. You have to print the cost of the optimal solution of the cutting problem, that is the minimum cost of cutting the given stick. Format the output as shown below.

Sample Input

100

3

25 50 75

10

4

4 5 7 8

0

Sample Output

The minimum cutting is 200.

The minimum cutting is 22.

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть массив m содержит точки распила: m₁, …, m_n. Добавим начальную и конечную точку: m₀ = 0, m_n+1 = l.

Пусть f(a, b) возвращает минимальную стоимость распила куска палки от m_a до m_b по требуемым точкам распила, находящимся внутри отрезка. Внутри отрезка [m_a; m_{a + 1}] точки распила отсутствуют, поэтому f(a, a + 1) = 0. Ответом на задачу будет значение f(0, n + 1). Вычисленные значения f(a, b) сохраняем в dp[a][b].

Пусть отрезок палки [m_a, m_b] следует распилить на несколько кусов. Пусть первый распил мы совершим в точке m_i (a < i < b). Тогда стоимость самого распила составит m_b – m_a, а далее следует оставшиеся куски распилить соответственно за цену f(a, i) и f(i, b). Значение i следует выбрать так чтобы минимизировать сумму:

f(a, b) = + m_b – m_a

Пример

Рассмотрим один из возможных методов распила стоимостью 10 + 7 + 3 + 3 = 23:

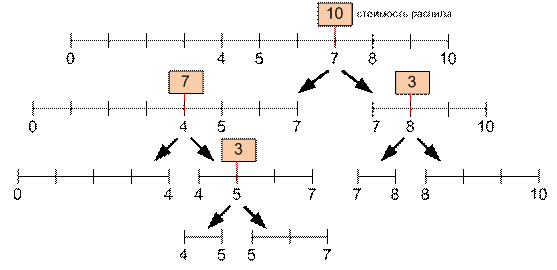
Рассмотрим оптимальный метод распила стоимостью 10 + 6 + 3 + 3 = 22:

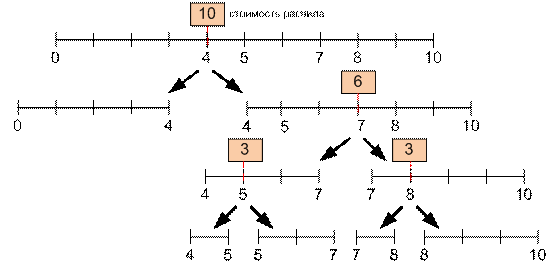
Реализация алгоритма

#include <stdio.h>

#include <string.h>

#define MAX 55

#define INF 0x3F3F3F3F

int dp[MAX][MAX];

int m[MAX];

int f(int a, int b)

{

if(b - a == 1) return 0;

if(dp[a][b] != INF) return dp[a][b];

for(int i = a + 1; i < b; i++)

{

int temp = m[b] - m[a] + f(a,i) + f(i,b);

if (temp < dp[a][b]) dp[a][b] = temp;

}

return dp[a][b];

}

int i, l, n;

int main(void)

{

while(scanf("%d",&l),l)

{

scanf("%d",&n);

m[0] = 0; m[n+1] = l;

for(i = 1; i <= n; i++)

scanf("%d",&m[i]);

memset(dp,0x3F,sizeof(dp));

printf("The minimum cutting is %d.\n",f(0,n+1));

}

return 0;

}